Принцип Дирихле

Рассмотрим следующую задачу.

Задача 1. В хвойном лесу растут 800000 елей. На каждой ели - не более 500000 иголок. Доказать, что существуют хотя бы две ели с одинаковым числом иголок.

Решение. Предположим противное, то есть, предположим, что в этом лесу не существуют две ели с одинаковым числом иголок. Тогда существует не более одной ели (одна ель или ни одной), имеющей одну иголку. Аналогичным образом, существует не более одной ели с двумя иголками и т.д., не более одной ели с 499999 иголками, не более одной ели с 500000 иголками. Таким образом, не более 500000 елей обладают числом иголок от 1 до 500000. Поскольку всего растут 800000 елей, и каждая ель имеет не долее 500000 иголок, следует, что найдутся хотя бы две ели с одинаковым числом иголок.

Замечание. Легко заметить, что решение в сути не зависит от конкретных чисел 800000 (количество елей) и 500000 (наибольшее число иголок). Принципиально был использован тот факт, что число 800000 строго больше 500000. В доказательстве предполагалось, что нет ни одной ели без иголок, хотя задача и доказательство справедливы и в этом случае.

Теперь сформулируем принцип Дирихле.

Пусть в n коробок помещены k предметов. Если количество предметов больше количества коробок (k > n), тогда существует хотя бы одна коробка, в которой бы находилось 2 предмета.

Примечание. Отметим, что не важно, в какой именно коробке находятся по крайней мере два предмета. Также не имеет значение, сколько предметов в этой коробке, и сколько всего таких коробок. Важно то, что существует хотя бы одна коробка с не менее чем двумя предметами (два или более).

В литературе этот принцип также встречается под названиями: "принцип кроликов и клеток", "принцип ящиков и объектов".

Вернемся к задаче 1. Решим эту задачу, используя принцип Дирихле. Пусть имеются 500000 коробок, соответственно пронумерованных 1,2,3,...,500000. Помещаем (мысленно) в эти коробки 800000 елей следующим образом: в ящик с номером s помещаем ели, на которых ровно s иголок. Поскольку елей, то есть "предметов", больше, чем коробок, следует, что по крайней мере одна коробка будет содержать не менее двух предметов, то есть, не менее двух елей. Так как в одной и той же коробке находятся ели с одинаковым числом иголок, приходим к выводу, что существуют хотя бы две ели с одинаковым числом иголок.

Конечно, задача 1, как мы убедились, очевидна, и легко может быть решена без помощи принципа Дирихле. Поэтому, естественно, возникает вопрос: "Для чего тогда нужен принцип Дирихле?" В дальнейшем мы увидим, что некоторые задачи не так очевидны при непосредственном решении, но в то же время достаточно просто решаются при помощи принципа Дирихле. Простота решения в значительной степени зависит от того, насколько удачно будут выбраны "коробки" и "предметы". То есть, при использовании принципа Дирихле необходимо указать, что (кто) будет "коробкой", а что (кто) - "предметом".

В дальнейшем, для закрепления материала, приведем решения ряда задач.

Задача 2. Доказать, что среди шести целых чисел найдутся два числа, разность которых делится на 5.

Решение. Рассмотрим 5 коробок, пронумерованных 0,1,2,3,4, - цифрами, представляющими собой остатки от деления на 5. Распределим в эти коробки шесть произвольных целых чисел в соответсвии с остатком от деления на 5, то есть, в одну и ту же коробку помещаем числа, имеющие одинаковый остаток от деления на 5. Поскольку чисел ("предметов") больше, чем коробок, согласно принципу Дирихле, существует одна коробка, содержащая более одного предмета. То есть, существуют (по крайней мере) два числа, помещенные в одну и ту же коробку. Следовательно, существуют два числа с одинаковым остатком от деления на 5. Тогда, разность этих чисел делится на 5.

Задача 3. Доказать, что для любого натурального числа n ≥ 1, существует натуральное число, состоящее из цифр 0 и 5, делящееся на n.

Решение. Рассмотрим натуральные числа

и распределим эти "предметы" в "коробки" пронумерованные 0,1,...,n-1 (цифрами, представляющими собой остатки от деления на n). В коробку s помещаем число a_k, которое имеет остаток от деления на n, равный s.

Если в коробке с номером 0 находится один "предмет" (то есть, одно число), тогда задача решена. В противном случае n "предметов" находятся в n-1 "коробках". Согласно приципу Дирихле, существуют два "предмета" (числа), находящиеся в одной и той же коробке. То есть, существуют два числа, имеющие одинаковый остаток от деления на n. Их разность будет делится на n, и как легко заметить, разность чисел, состоящих из цифр 0 и 5, также будет числом, состоящим из 0 и 5.

Задача 4. В зале находятся n человек (n ≥ 2). Доказать, что среди них найдутся два человека с одинаковым числом знакомых (предполагается, что если человек A является знакомым человека B, то и B является знакомым A; никто не считается своим собственным знакомым).

Рещение. Обозначим через m количество человек, которые имеют хотя бы одно знакомство в зале (это и будут "предметы"). Каждый из этих m человек может иметь 1,2,...,m-1 знакомых ("коробки" - число знакомых).

Согластно принципу Дирихле, сущетсвуют два человека с одинаковым числом знакомых.

При решении некоторых задач полезно применять обобщенный принцип Дирихле.

Если pn+1 предметов поместить в n коробок, тогда хотя бы одна коробка будет содержать по крайней мере p+1 предметов.

Задача 5. В доме живут 40 учеников. Существует ли такой месяц в году, когда хотя бы 4 ученика празднуют свой день рождения.

Решение. Пусть "коробками" будут месяцы, а "предметами" - ученики. Распределяем, "предметы" по "коробкам" в зависимости от месяца рождения. Так как число месяцев, то есть, коробок, равно 12, а число учеников, то есть, предметов 40 = 12·3+4, согласно принципу Дирихле существует коробка (месяц) с по крайней мере 3+1=4 предметами (учениками).

Задача 6. Пусть M - множество, состоящее из n целых чисел. Доказать, что существует подмножество M₁ множества M такое, что сумма элементов множества M₁ делилась бы на n.

Решение. Пусть M = {a₁,a₂,...,a_n}. Рассмотрим следующие суммы

S₁ = a₁,

S₂ = a₁ + a₂,

...

S_n = a₁ + a₂ + ... + a_n.

Если одно из чисел S_k (k = 1,...,n) не делится на n, тогда остатки от деления на n будут 1,2,...,n - 1. Так как имеются n сумм и n - 1 остатков, то по крайней мере две суммы дадут одинаковый остаток от деления на n. Пусть S_k и S_m (1 ≤ k < m ≤ n) - две из них. Тогда S_m - S_k делится на n, и искомое множество есть {a_k+1, ... ,a_m}.

Задача 7. Доказать, что из n+1 различных натуральных чисел, меньших 2n, можно выбрать 3 числа так, чтобы одно число было равно сумме двух других.

Решение. Пусть a₁ < a₂ < ... < a_n+1 - данные числа. Рассмотрим разности

a₂ - a₁,

a₃ - a₁,

...

a_n+1 - a₁.

Эти числа различны, положительны и меньшие, чем 2n. Согласно принципу Дирихле, хотя бы два числа совпадают. Более того, одно из этих чисел принадлежит множеству {a₂ - a₁, ... ,a_n+1 - a₁}. Пусть это будут числа a_k и a_m - a₁. Отсюда a_k = a_m - a₁, и, следовательно, a_m = a_k + a₁.

Задача 8. Пусть a₁,a₂, ... ,a_n - перестановка чисел 1,2,3,...,n. Доказать, что произведение (a₁ - 1)(a₂ - 2)...(a_n - n) будет четным, если n - нечетно.

Решение. Пусть n = 2k + 1. Во множестве рассмотренных чисел k + 1 чисел будут нечетными. В исходном произведении среди уменьшаемых и вычитаемых будут (k + 1) + (k + 1) = 2(k + 1) = n + 1 нечетных чисел. Поскольку произведение состоит из n сомножителей, один (по крайней мере) из них будет содержать только нечетные числа (и уменьшаемое и вычитаемое будут нечетными). Таким образом, этот множитель будет четным, и произведение также будет четным.

Задача 9. В 500 коробках лежат яблоки. Известно, что в каждой коробке находятся не более 240 яблок. Доказать, что существуют хотя бы 3 коробки, которые содержат одинаковое количество яблок.

Решение. Пусть в первых 240 коробках находится различное количество яблок (1,2,...,240) , в следующих 240 коробках - аналогично (то есть, анализируется экстремальный случай; более подробно об этом методе рассказывается в теме "принцип крайнего"). Таким образом, остались 500 - 2·240 = 20 коробок, в которые необходимо поместить яблоки от 1 до 240.

Задача 10. В коробке лежат 10 красных карандашей, 8 синих, 8 зеленых и 4 желтых. Наугад (произвольно) из коробки вынимают n карандашей. Определить наименьшее число карандашей, которые необходимо вынуть, чтобы среди них было:

a): не менее 4 карандашей одного цвета;
b): по одному карандашу каждого цвета;
c): хотя бы 6 карандашей синего цвета.

Решение. a) Пусть вынули 13 карандашей. Так как у нас всего 4 цвета, согласно принципу Дирихле (карандаши будут "предметами", а цвета - "коробками"), по крайней мере 4 карандаша будут одинакового цвета.

Докажем, что n = 13 является наименьшим числом. С этой целью покажем ситуацию, при которой условия задачи не выполняются. Например, когда вынуто по 3 карандаша каждого цвета (12 карандашей). Отметим, что эта ситуация возможна, так как в коробке находится не менее 3 карандашей каждого цвета.

Случаи b) и с) решаются аналогично.

Задача 11. В международном симпозиуме участвуют 17 человек. Каждый знает не более трех языков и любые два участника могут общаться между собой. Доказать, что хотя бы три участника, знают один и тот же язык.

Решение. Пусть A - один из участников. Он может общаться с каждым из 16 участников на не более одном из трех известных ему языков. Тогда существует язык, на который A говорит с не менее чем шестью участниками. Пусть B - любой из них. Ясно, что среди остальных 5 участников есть 3, с которыми B может общаться на одном языке (назовем его "второй язык"). Если среди этих троих участников хотя бы два, скажем C и D, могут говорить на "втором языке", то B, C и D и есть те три человека, говорящие на одном языке.

Некоторые задачи, в особености геометрические, решаются при использовании принципа Дирихле в следующих формулировках:

a): Если на отрезке длиной l расположены несколько отрезков, сумма длин которых больще l, тогда по крайней мере два отрезка имеют общий точку;
b): Если внутри фигуры площадью S расположены фигуры, сумма площадей которых больше S, тогда среди них существуют хотя бы две фигуры, имеющие общую точку;
c): Если фигуры F₁,F₂, ... ,F_n S₁,S₂, ... ,S_n - соответственно их площади) расположены в фигуре F площадью S и S₁ + S₂ + ... + S_n > kS, тогда k + 1 из фигур F₁,F₂, ... ,F_n имеют общую точку.

Задача 12. Точки на плоскости раскрашены двумя цветами. Показать, что существуют две точки одинакового цвета, расположенные на расстоянии 1м.

Решение. Рассмотрим равносторонний треугольник со стороной 1м. Вершины треугольника будут "предметами", а цвета - "коробками". Так как число "предметов" больше числа "коробок", следует, что существуют две вершины одного цвета. Поскольку треугольник равносторонний, расстояние между вершинами составляет 1м.

Отметим, что эта задача может быть решена и другим методом - от противного. Пусть A - одна из точек плоскости, и предложим, что все точки плоскости, расположенные на растоянии 1м от A, окрашены в цвет, отличный от цвета точки A. Тогда получаем окружность радиуса 1 из точек одинакового цвета. Очевидно, что в этой окружности существует хорда длиной 1м. Следовательно, концами хорды будут точки одного цвета, расположенные на растоянии 1м.

Задача 13. На плоскости даны n различных точек. Пара точек определяет отрезок. Доказать, что существуют две точки, из которых выходит одинаковое число отрезков.

Решение. Из одной точки может выходить максимум n - 1 отрезков и минимум 1 отрезок. Поскольку имеются n точек, то найдутся две такие, из которых выходит одинаковое число отрезков.

Задача 14. Внутри квадрата со стороной 1 находятся несколько окружностей, сумма длин которых равна 10. Показать, что существует прямая, пересекающая не менее четырех из этих окружностей.

Решение. Проецируем окружности на одну из сторон квадрата. Проекция каждой окружности представляет собой отрезок, длина которого равна диаметру соответствующей окружности. Сумма этих отрезков равна Согласно принципу Дирихле, существуют хотя бы четыре отрезка, имеющие общую точку. Перпендикуляр, проведенный из этой точки на сторону квадрата, пересечет не менее четырех окружностей.

Задача 15. Внутри равностороннего треугольника со стороной 1 лежат 5 точек. Доказать, что найдутся две точки из пяти, расстояние между которыми меньше 0,5.

Решение. Делим равносторонний треугольник со стороной 1 на четыре равносторонних треугольника со стороной 0,5 (рис. 1).

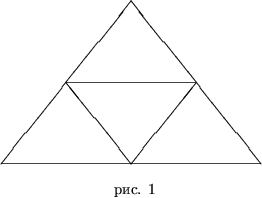
В одном из этих четырех треугольников лежат по крайней мере две из данных точек. Расстояние между этими двумя точками меньше 0,5.

Задача 16. На плоскости даны 25 точек таким образом, что две точки из любых трех расположены на расстоянии меньше 1. Доказать, что существует круг радиуса 1, содержащий не менее 13 из данных точек.

Решение. Пусть A - одна из данных точек. Если остальные точки находятся внутри круга S₁ радиуса 1 с центром в точке A, тогда задача решена. Пусть B - одна из точек, лежащих вне круга S₁. Рассмотрим круг S₂ радиуса 1 с центром в точке B. Среди точек A, B, C, где C - произвольная из данных точек, существуют две, расстояние между которыми меньше 1. Более того, этими точками не могут быть A и B.

Таким образом, круги S₁ и S₂ содержат все исходные точки. То есть, один из этих кругов содержит не менее 13 точек.

Задача 17. На плоскости даны n попарно непараллельных прямых. Показать, что существуют прямые, угол между которыми составляет менее

Решение. Выбираем на плоскости точку, через которую проводим прямые, параллельные данным n прямым. Эти прямые разбивают плоскость на 2n углов, сумма величин которых равна 360^°. То есть, по крайней мере один из углов будет меньше

Задача 18. На бесконечную сетку помещена фигура, площадь которой меньше площади квадратика сетки. Доказать, что эта фигура может быть размещена на сетке так, чтобы она не покрывала узлы сетки.

Решение. Размещаем данную фигуру на сетке произвольным образом и разрезаем сетку вдоль сторон. Складываем все квадратики сетки один на другой, образуя стопку, при этом совершая только параллельные перемешения (без поворотов). Проецируем фигуру на один квадратик. Проекции фигуры не могут покрывать весь квадратик, так как его площадь больше площади фигуры. Возвращаемся к исходному положению фигуры и переносим сетку параллельно, таким образом, чтобы проекции вершин располагались внутри фигуры. В результате мы получим искомое положение фигуры.

Самостоятельная работа

Доказать, что из 11 цифр можно выбрать две одинаковые.
Показать, что из трех чисел, отличных от нуля, два числа будут одного знака.
Доказать, что в школе, где учатся 400 учеников, найдутся двое, дни рождения которых совпадают.
Доказать, что существует число вида 1999 1999... 1999 00... 00, делящееся на 1999.
Доказать, что любое множество, состоящее из 2ⁿ⁺¹ - 1 целых чисел содержит подмножество из 2ⁿ чисел, сумма которых делится на 2ⁿ.
Показать, что существует натуральное число делящееся на 1997, последние цифры которого 1998.
В национальном чемпионате по футболу участвуют 30 команд. Доказать, что в любой момент найдутся две команды, которые сыграли одинаковое количество игр в чемпионате.
Показать, что среди любых (n + 2) натуральных чисел найдутся два числа, сумма либо разность которых делится на 2n.
Показать, что среди n + 1 натуральных чисел, меньших 2n, есть два числа, отношение которых является степенью числа 2.
Показать, что среди любых трех простых чисел, больших 3, можно выбрать два числа, сумма либо разность которых делится на 12.
Показать, что, какими бы ни были числа a, b, c, d, число abcd(a² - b²)(a² - d²)(b² - c²)(b² - d²)(c² - d²) кратно семи.
Доказать, что для любого натурального числа существует кратное этого числа, записанное только цифрами 0 и 1.
Пусть n О N, n > 1. Показать, что любые n + 2 числа из множества {1,2,...,3n}, содержат два, разность которых заключена в интервале (n,2n).
Узлы бесконечной сетки выкрашены в два цвета. Доказать, что существуют две вертикальные и две горизонтальные прямые, пересечение которых содержит точки одинакового цвета.
В прямоугольнике 3×4 взяты 6 точек. Доказать, что среди них существуют две, расстояние между которыми меньше .
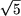В квадрате со стороной 1 расположены 51 точек. Доказать, что три из этих точек могут быть покрыты кругом радиуса ¹/₇.
Показать, что в любом выпуклом 2n-угольнике существует диагональ, не параллельная ни одной из его сторон.
Определить минимальное число точек, которые необходимо выделить в выпуклом n-угольнике, чтобы любой треугольник с вершинами в вершинах многоугольника содержал хотя бы одну выделенную точку.
В круге радиуса 1 проведено несколько хорд. Доказать, что если каждый диаметр пересекает не более S хорд, то сумма длин хорд меньше pS.
В круге радиуса 16 взяты 650 точек. Доказать, что существует кольцо, больший радиус которого равен 3, а меньший - 2, содержащее более 10 точек из данных.
Показать, что грани куба не могут быть выкрашены в два цвета таким образом, чтобы любые две соседние грани были разного цвета.
В кубе с ребром 1 помещены m³ + 1 точек. Показать, что существуют по крайней мере две точки, расстояние между которыми меньше
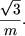
Доказать, что в любом девятиугольнике существует пара диагоналей, угол между которыми меньше 7^°.
Даны две окружности, длиной по 100см. На одной из окружностей выделены 100 точек, а на другой - несколько дуг, сумма длин которых меньше 1. Доказать, что окружности могут быть наложены друг на друга таким образом, чтобы ни одна из выделенных точек не попала на выделенную дугу.

Литература

Mircea Ganga, Teme si probleme de matematica, Ed. Tehnica, Bucuresti, 1991, 331p.
V.A.Ufnarovski, Acvariu Matematic, "Stiinta", Chisinau, 1988, 237p.
В.В.Прасолов, Задачи по планиметрии, ч.2, Москва, Наука, 1991, 139стр.
И.Л.Бабинская, Задачи математических олимпиад, Москва, Наука, 1975, 112стр.
V.A.Gusev, A.I.Orlov, A.L.Rozental, Lucrul in afara orelor de curs la matematica in clasele VI-VIII, Chisinau, Lumina, 1980, 293p.