Bacalaureat 2002, Profilul real

Ministerul Invatamantului al Republicii Moldova
Examenul de bacalaureat la matematica, 2002
Profilul real

Timp alocat: 180 minute.

1. Determinati valoarea de adevar a propozitiei "(") x Î R, x² + 9 – 6x > 0 ".

2. Calculati

3. In acelasi reper cartezian de coordonate, reprezentati grafic functiile f, g : [–3,3] ® R, astfel incat f(x) < g(x) si f '(x) > g'(x).

4. Determinati distanta de la centrul cercului de ecuatie x² + y² + 6x + 10y – 135 = 0 pana la originea axelor de coordonate.

5. Pentru ce valori reale ale lui x si y numerele z₁ = x² + 4y – yi si sunt conjugate?

6. Rezolvati ecuatia

7. Determinati intervalele de monotonie ale functiei f : R ® R,

8. Raportul dintre aria bazei unui con circular drept si aria sectiunii axiale este egal cu p. Determinati masura unghiului format de generatoare si planul bazei.

9. Determinati radacinile polinomului P(X) = X ³ – 15X ² + 74X – 120, daca se stie ca una din radacini este media aritmetica a celorlalte doua radacini.

10. Unui trapez i se circumscrie un cerc. Masura unghiului format de baza mare si latura laterala este a, iar masura unghiului format de aceeasi baza si diagonala este b. Determinati raportul dintre aria discului marginit de cerc si aria trapezului.

11. Se considera functia f : [0,2] ® R, f(x) = 2x – x². Determinati parametrul real m, astfel incat dreapta de ecuatie y = mx sa imparta subgraficul functiei in doua multimi de arii egale.

12. Pentru care valori ale parametrului real a ecuatia a (2^x + 2^–x) = 5 admite o singura radacina?

Solutii

1. Propozitie falsa. Se observa ca x² + 9 – 6x = (x–3)² si cum pentru x = 3 se obtine (x–3)² = 0, rezulta ca $ x, x = 3 Î R astfel incat x² + 9 – 6x nu este strict mai mare ca zero.

3. De exemplu:

In adevar, cum g este strict descrescatoare, avem g'(x) < 0 si, cum f este strict crescatoare, f '(x) > 0, prin urmare g'(x) < f '(x) (xÎ [–3,3]).

4. Se determina ecuatia canonica a cercului:
x² + y² + 6x + 10y – 135 = 0 Û (x² + 6x + 9) – 9 + (y² + 10y + 25) – 25 – 135 = 0 Û
Û (x+3)² + (y+5)² = 169.
Rezulta, coordonatele centrului cercului O₁(–3; –5). Se utilizeaza formula distantei dintre doua puncte date si se obtine:

5.

Cum implica rezulta de unde y = 1 si x² = 1, adica x = ± 1, y = 1.
Raspuns: x = 1, y = 1 sau x = –1, y = 1.

7. Se determina derivata functiei f :

Se determina punctele critice functiei f : f'(x) = 0 Þ x = 0 (se observa ca pentru " xÎ R $ f '(x)).
Se determina semnul derivatei si intervalele de monotonie: pentru x < 0, f '(x) > 0 si deci pentru xÎ(– ¥,0] functia este crescatoare, pentru x > 0, f '(x) < 0 si, prin urmare, pentru xÎ[0, + ¥) functia este descrescatoare.

8.

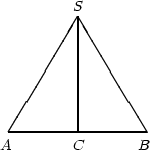
Fie BC = AC = r – raza conului, SB = l – generatoarea lui, SC = h – inaltimea.
Cum si rezulta adica r = h. Asadar triunghiul dreptunghic SCB este isoscel si, deci Ð SBC (dintre generatoare si planul bazei) este egal cu 45^o.

9. Se utilizeaza teorema Viette, conditia problemei si se obtine:

10.

Cum trapezului ABCD i se circumscrie un cerc, rezulta ca trapezul este isoscel. Prin urmare Ð DAB = Ð CBA = a, AC = BD. Atunci Ð DBC = a-b. Fie raza cercului R. Se utilizeaza teorema sinusurilor si se obtine:

CD = 2Rsin(a - b)
AB = 2R sin(180^o – (a + b)) = 2Rsin(a + b).

Fie DE = h – desemneaza inaltimea trapezului. Atunci

DE = BD sinb = 2Rsina × sinb

si astfel

= 2R² sin²a × sin2b.

Prin urmare:

11.

Se determina aria subgraficului functiei f :

Se determina abscisa punctului C:

2x – x² = mx Þ x² + (m – 2)x = 0 Þ

é
ë

x₁ = 0,

x₂ = 2 – m.

Cum x₂ Î [0,2] Þ 0 ≤ 2 – m ≤ 2, de unde m Î [0,2].
Se determina aria figurii marginite de graficele functiilor f(x) = 2x – x² si y = mx:

Cum

se obtine

de unde (2 – m)³ = 4, 2 – m =

, deci m = 2 –

. Se observa, ca m = 2 –

Î [0,2], adica verifica conditiile problemei.
Raspuns: m = 2 –

12. Cum 2^x + 2^–x > 0, rezulta ca ecuatia admite solutii numai pentru a > 0. Atunci ecuatia se scrie

2^x + 2^–x = ⁵/_a .

Cum functia f : R ® R, f(x) = 2^x + 2^–x este o functie para si strict crescatoare, ultima ecuatie are o singura solutie daca si numai daca x = 0, de unde a = ⁵/₂.

Schema de notare Scor maxim
    Nr. 1 – 2 puncte
    Nr. 2 – 4 puncte
    Nr. 3 – 4 puncte
    Nr. 4 – 4 puncte
    Nr. 5 – 5 puncte
    Nr. 6 – 6 puncte
    Nr. 7 – 5 puncte
    Nr. 8 – 6 puncte
    Nr. 9 – 7 puncte
    Nr. 10 – 9 puncte
    Nr. 11 – 10 puncte
    Nr. 12 – 10 puncte
    total: 72 puncte

Nota
    "10" – 69-72 puncte
    "9" – 63-68 puncte
    "8" – 54-62 puncte
    "7" – 42-53 puncte
    "6" – 31-41 puncte
    "5" – 23-30 puncte
    "4" – 15-22 puncte
    "3" – 7-14 puncte
    "2" – 2-6 puncte
    "1" – 0-1 puncte